Em abril deste ano, a rede neural do DeepMind da Google tirou E em uma prova de matemática do Ensino Médio (não conseguiu sequer somar 1 + 1 + 1 + 1 + 1 + 1 + 1). Onde a Google falhou, o Facebook triunfou, ao treinar uma rede neural para executar o raciocínio simbólico necessário para diferenciar e integrar expressões matemáticas.
Os pesquisadores Guillaume Lample e François Charton, da Facebook AI Research em Paris (França), em um artigo no arXiv Research, afirmam que conseguiram treinar uma rede neural para que ela resolvesse equações complexas com símbolos, como x e y.
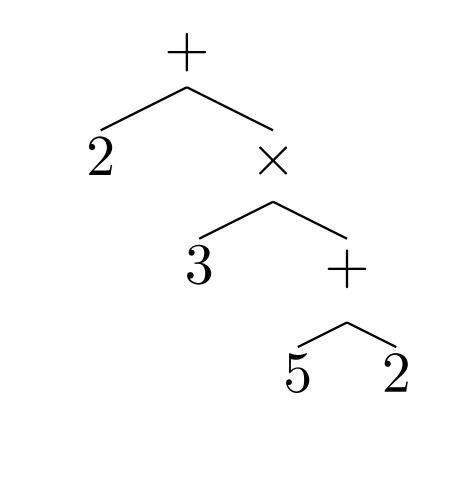
O que Lample e Charton fizeram foi ensinar a IA a identificar a hierarquia contida em expressões matemáticas. Usando o exemplo dado no estudo, para resolver a equação 2 + 3(5 + 2), precisamos resolver a sequência (5 + 2), depois multiplicar o resultado por 3 e, finalmente, adicionar 2. A IA precisa identificar esses padrões, simplificar as expressões e resolvê-las.
Lample e Charton dividiram as expressões matemáticas em partes, representando-as como árvores. (Fonte: MIT Technology Review(Reprodução)
Foram criadas expressões com 15 partes, usando as quatro operações binárias e quinze operações unárias (exp, log, sin, cos, tan etc). A cartilha da IA reuniu 80 milhões de equações diferenciais de primeiro e segundo grau e 20 milhões de expressões integradas.
Aprendizado além do esperado
A IA não apenas aprendeu a resolver as equações como também a derivar e integrar uma expressão matemática complexa. Os pesquisadores ainda testaram a IA com cinco mil expressões desconhecidas por ela e compararam os resultados com os do Maple, Matlab e Mathematica (softwares usados para resolver problemas matemáticos).
A rede neural do Facebook conquistou com louvor um A: precisão próxima de 100% em tarefas como a integração de funções (o Mathematica não passou dos 85%) e tempo de cálculo não superior a um segundo (os softwares precisam de mais de meio minuto para alcançar a resposta certa).
A rede neural ainda descobriu mais de uma solução para cada problema. "A capacidade do sistema de recuperar expressões equivalentes, sem ser treinado para isso, é muito intrigante e ainda um mistério", disse Lample.
Fonte:MIT Technology Review


Nenhum comentário:
Postar um comentário